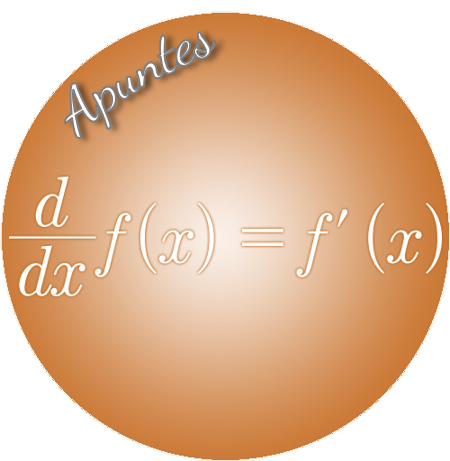Apuntes de Matemáticas de Ciencias Sociales de 2º Bachillerato
Este último curso del instituto es muy importante para ti. Cuando lo finalices realizarás el examen de acceso a la Universidad, por eso es muy importante que vayas asimilando muy bien cada tema. Cuanto más le dediques ahora, menos tendrás que repasarlo al finalizar el año.
Para poder entender bien la asignatura de Matemáticas de Ciencias Sociales y poder enfrentarte a cualquier tipo de problema, es fundamental tener unos buenos apuntes de estudio.
Durante estos años como profesora he ido haciendo un material adaptado a las clases que imparto a mis alumnos. Se trata de unos apuntes fáciles de entender con ejemplos para facilitarte la comprensión y con todo el material necesario para sacar la máxima nota en los exámenes.
Todo el material está disponible para que puedas visualizarlo sin problema. En caso de que necesites descargarlo, puedes ponerte en contacto conmigo y te diré los pasos a seguir.
En todas las comunidades autónomas se dan los mismos temas en Matemáticas de Ciencias Sociales, así que puedes utilizar este material independientemente de dónde te examines.
Cualquier duda que tengas al respecto puedes hacérmela llegar o bien en opiniones o bien contactando conmigo. Puedes preguntarme sin ningún tipo de compromiso.
Son diez los temas que componen la asignatura de Matemáticas de Ciencias Sociales de 2º de Bachillerato, están divididos en tres bloques: álgebra, análisis y estadística.
Bloque I.- ÁLGEBRA
Tema 1.- Álgebra de Matrices
Empezaremos este curso hablando de las matrices, las definiremos, veremos los tipos que existen, aprenderemos a operar con ellas: suma, resta y multiplicación de matrices, multiplicación por un número, transposición y potencia n–ésima de una matriz. Hablaremos de la matriz inversa y aprenderemos a calcularla mediante su definición, esta matriz inversa es muy importante para poder solucionar ecuaciones matriciales. Acabaremos el tema hablando del rango de una matriz, aprenderemos a calcularlo mediante Gauss, este último punto es muy importante que lo entiendas para luego comprender bien el tercer tema de este bloque dedicado a los sistemas de ecuaciones lineales.
Tema 2.- Los Determinantes
En este segundo tema aprenderemos que un determinante es el valor numérico asociado a cada matriz cuadrada. Aprenderemos a calcular los determinantes de matrices cuadradas de orden dos, tres y superior. Estudiaremos las propiedades de los determinantes y a usarlos para calcular la matriz inversa y el rango de una matriz.
Tema 3.- Sistemas de Ecuaciones Lineales
El año pasado ya aprendimos a resolver sistemas de ecuaciones lineales con tres incógnitas mediante el método de Gauss. Este año vamos a aprender a expresar los sistemas de ecuaciones en forma matricial y a clasificarlos usando los rangos de la matriz de los coeficientes y la matriz ampliada, según el número de soluciones que tengan en sistemas incompatibles (sin solución), sistemas compatibles determinados (una única solución) y compatibles indeterminados (infinitas soluciones). Aprenderemos un nuevo método para resolver sistemas compatibles determinados, el método de Cramer que emplea determinantes.
Tema 4.- Programación Lineal
Los problemas de programación lineal se usan en los procesos de toma de decisión de numerosos ámbitos económicos y productivos. Aprenderemos en qué consiste un programa lineal o programa de programación lineal. Veremos que el objetivo de este tipo de problemas es la optimización de una función llamada objetivo, podemos maximizarla o minimizarla. Esta optimización se realiza mediante una serie de restricciones que no son más que un sistema de inecuaciones lineales y su representación gráfica para obtener la región factible. Existen varios tipos de programas lineales dependiendo del número de soluciones que tengan, en este curso sólo nos interesan los factibles de solución única, siendo ésta uno de los vértices que forman la región factible.
Bloque II.- ANÁLISIS
Tema 5.- Límites, Continuidad y Asíntotas
Empezaremos este bloque de análisis repasando los límites: El año pasado ya aprendimos a trabajar con algunas indeterminaciones (∞/∞, 0/0, ∞–∞, 1∞), las repasaremos y aprenderemos a trabajar con algunas más (∞0, 0∞, ∞·0). Repasaremos cómo se estudia la continuidad de una función y aprenderemos a clasificar los tipos de discontinuidades en evitables, inevitables de salto finito e inevitables de salto infinito. Por último, aprenderemos a calcular y qué significan los tres tipos de asíntotas que puede tener una función: verticales, horizontales y oblicuas. Todo este tema es muy importante que lo entiendas para que luego no tengas problemas a la hora de representar gráficamente distintos tipos de funciones.
Tema 6.- Las Derivadas y sus Aplicaciones
El año pasado empezamos a derivar funciones simples, este año nos metemos de fondo y acabaremos el tema siendo capaces de hacer derivadas de funciones complejas, simplemente aplicando la regla de la cadena y teniendo en cuenta las operaciones con derivadas. Pero primero, empezaremos el tema definiendo lo que es la derivada de una función y su interpretación gráfica. Además, aprenderemos a estudiar la derivabilidad de una función. Por último, estudiaremos distintas aplicaciones de las derivadas como la recta tangente de una función en un punto, el estudio del crecimiento de una función con sus extremos relativos, el estudio de la curvatura de una función con sus puntos de inflexión, la optimización de funciones con los problemas de optimización y finalmente, veremos cómo se hace el estudio completo y la representación de funciones.
Tema 7.- Las Integrales y sus Aplicaciones
Primero decirte que este tema no todos los profesores lo imparten ya que no en todas las comunidades autónomas forma parte del temario para la EvAU. Si eres de los que tienen la suerte de que tu profesor te dé este tema te diré que aprenderás a hacer integrales inmediatas, con cambio de variable y por partes. Además, estudiarás lo que es una integral definida y las usarás para calcular áreas de recintos planos delimitados por funciones y los ejes de abscisas o entre funciones.
Bloque III.- ESTADÍSTICA
Tema 8.- Combinatoria y Probabilidad
Este último bloque está compuesto por tres temas, en este primero vamos a empezar hablando de la combinatoria (combinaciones, variaciones y permutaciones) que es una forma de contar situaciones que se pueden dar en un experimento aleatorio. Seguiremos estudiando estos experimentos aleatorios y los sucesos asociados a ellos, además de repasar las distintas operaciones que se pueden hacer con dichos sucesos. Definiremos lo que es la probabilidad y veremos cómo calcularla en distinto tipos de experimentos aleatorios (simples con diagramas de Venn y compuestos con diagramas de árbol). Dentro de los experimentos compuestos vamos a estudiar la probabilidad condicionada y dos teoremas: el teorema de la probabilidad total y el teorema de Bayes.
Tema 9.- Distribuciones de Probabilidad
En este tema nos vamos a dedicar a estudiar dos distribuciones de probabilidad, que no es más que un modelo teórico que explica el comportamiento de un fenómeno real. La primera distribución es la Binomial y está asociada a variables aleatorias discretas (aquellas que no pueden tomar valores decimales) y la segunda es la distribución Normal que es la más usada porque está asociada a variables aleatorias continuas que son las más frecuentes.
Tema 10.- Intervalos de Confianza
Y acabaremos el curso con un tema que pertenece a la estadística inferencial que se ocupa de predecir qué es lo que va a ocurrir en una población a partir de los datos extraídos de una muestra. Empezaremos viendo un poco cómo se hace el muestreo para obtener dicha muestra, lo cual es un paso fundamental para que el estudio estadístico sea fiable. Después estudiaremos los intervalos de confianza para la media de una población y los intervalos de confianza para una proporción.
Y fin... Espero haberte ayudado en tu estudio de las Matemáticas de Ciencias Sociales de 2º de Bachillerato, si ha sido así te agradecería enormemente que me dejaras algún comentario al respecto..
Muchas gracias!!